Prueba de Proposiciones

💢 28 de junio, 2019:

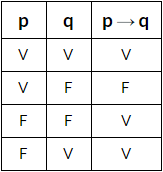
💭 El día de hoy tuvimos nuestra tercer prueba del curso, la cual abarcaba el tema de las proposiciones; en donde se evaluó el manejo de éstas por medio de diversas maneras, entre las que se encontraba: clasificar oraciones como proposición simple, proposición compuesta, no proposición o proposición abierta; encontrar el valor de alguna de nuestras variables según los datos que se nos eran dados y utilizando los valores de verdad, dependiendo de la clase de proposición compuesta a la que la oración pertenecía; hallar el valor de verdad de cierta proposición; aplicar las leyes de De Morgan en ciertas oraciones; y escribir las oraciones condicionales en su forma inversa, recíproca y contrapositiva.

💬 En lo personal, el examen me pareció muy completo y lo suficientemente sencillo para ser finalizado en el tiempo estimado.

Entre las series que en él se hallaban, la que más se me dificultó fue la de hallar el valor de alguna de las variables que se nos daba dentro de una proposición; en donde nos teníamos que guiar por el valor de verdad que se nos indicaba que resultaría de operar los valores de la proposición, según su tipo, y los valores que representaban las variables de las cuales sí se nos eran indicados los datos; ya que todo este proceso necesitó de mucha concentración y de saber las reglas para encontrar los valores de verdad en cada tipo de proposición, para saber utilizar el correcto.

👉Una recomendación que yo daría para que la resolución del examen no se nos complique tanto es ir escribiendo o repasando mentalmente los chivos que nos aprendimos anteriormente sobre cada uno de los tipos de proposición, y leer detalladamente todo el examen para que no se nos pase por alto ningún dato que luego nos resulte necesario y cuya ausencia nos dificulte hallar la solución al problema correspondiente.

👤 Un ejemplo similar al que venía en el examen es:

• Identificar si la siguiente oración es una proposición, ya sea, abierta, compuesta, simple, o si no es una proposición:

- Toma las pastillas cada dos horas.

Respuesta: No es una proposición, porque es una oración imperativa, es decir una orden; por lo que no la podemos calificar como enunciado falso o verdadero.

Proposición: bicondicional

💢 27 de junio, 2019

💭 Este día vimos las proposiciones bicondicionales y su aplicación con las Leyes de De Morgan.

El punto visto este día me resultó sumamente fácil aunque co un procedimiento un tanto más largo en las Leyes de De Morgan que los usados con los otros tipos.

💬 Las bicondicionales se escriben usando el conector "si y solo si", y su símbolo es ⇿.

Su tabla de valores de verdad es:

👉 El chivo de esta proposición es saber que cuando ambos valores son falsos o ambos so verdaderos, el resultado será verdadero. 

Lógicamente, ambos enunciados deben tener el mismo valor, pues las bicondicionales presentan dos condiciones para existir, y si una de ellas no cumple con lo dicho en la otra, se deduce que los enunciados son incorrectos.

Su Ley de De Morgan:

Ejemplo;
p= Ana es vegetariana.
q= Ana ama a los animales.

~ (Ana es vegetariana si y solo si ama a los animales).

EQUIVALE A:

Ana es vegetariana y no ama a los animales, o, ama a los animales y no es vegetariana.

Proposición: condicional

💢 26 de junio 2019

💭 El día de hoy vimos la proposición de tipo condicional, sus partes y sus variaciones. Así también las Leyes de De Morgan aplicadas en ella.

Comprender la estructura de las condicionales y aplicarles la Ley de De Morgan, no me resultó complicado, sin embargo, aprenderme todos sus tipos de variaciones sí, por lo que aconsejo que los analicen lógicamente hasta hallarles coherencia a cada uno, y así poder relacionar el nombre de la variación con su forma de ser.

💬 Las condicionales se leen "Si... entonces" y su símbolo es ⇒

La primer parte que compone la oración es llamada antecedente (comienza siempre con el "si"), cuya función es poner la condición; y la que indica qué sucederá si se cumple o no dicha condición es la segunda parte, llamada consecuente.

A veces la consecuencia puede ser dicha antes de la condición.

Su tabla de valores es:

👉El chivo es aprenderse que solo cuando el antecedente es verdadero y el consecuente falso, el valor será falso.

Es importante saber que a diferencia de los otros tipos, las condicionales pueden presentar variaciones al momento de escribirlas, pero su valor de verdad permanece.

Las variaciones son:

Ejemplo: p= La blusa es roja. q= El sombrero es amarillo.

En forma directa: Si la blusa es roja, entonces el sombrero es amarillo.

Recíproca: Si el sombrero es amarillo, entonces la blusa es roja.

Inversa: Si la blusa no es roja, entonces el sombrero no es amarillo.

Contrapositiva: Si el sombrero no es amarillo, entonces la blusa no es roja.

Ley de De Morgan para condicionales:

Proposiciones: conjunción y disyunción, y Leyes de De Morgan

💢 24 de junio 2019

💭El día de hoy vimos dos clasificaciones de las proposiciones compuestas: disyunción y conjunción.

Y aprendimos a aplicarlas con las Leyes de De Morgan.

💬 Disyunción y Conjunción:

- Disyunción: cuando se nos da dos proposiciones

  (p o q) y su símbolo es p v q.

- Conjunción: cuando se nos da dos proposiciones (p y q), y su símbolo es p ^ q.

A continuación se mostrará la tabla para saber los valores de verdad de las disyunciones y otra de las conjunciones.

👉 El chivo es aprenderse que cuando es una conjunción (p y q) ambas necesitan ser verdaderas para que el valor sea verdadero: V y V, pues si uno o los dos enunciados son falsos, la proposición ya no puede ser verdadero.

En la disyunción (p o q) el chivo está en aprenderse que únicamente cuando ambas son falsas, el valor es falso. 

Como se usa el conector "o", lógicamente si uno es falso pero luego nos dicen uno verdadero, o ya sea que ambos sean verdaderos, nos están diciendo dos opciones, en donde hay uno o más verdaderos, por lo que la frase sería verdadera.

👤 Leyes de De Morgan:

Son utilizadas cuando se quieren encontrar equivalentes para proposiciones que se obtienen por negación de proposiciones compuestas.

Estas leyes son diferentes para cada tipo de proposición, por lo que es importante aprendérselas.

EN EL CASO DE LAS PROPOSICIONES YA VISTAS, SU APLICACIÓN RESPECTIVA DE ESTAS LEYES ES:

Disyunción: Será la negación de p con la conjunción de la negación de q, es decir:

     ~(pvq) equivale a negación de p y negación de q 

     (~p ^ ~q).

Conjunción: la disyunción de las negativas.

~(p ^ q) equivale a la negación de p o la negación de q

(~p v ~q)

Segunda prueba sobre los temas vistos en clase

💢 19 de junio

💭 El día de hoy, tuvimos nuestra segunda prueba sumativa, en la que evaluamos nuestra destreza para resolver los tipos de problemas vistos, utilizando los cuatro pasos del Método de Polya. 

Los problemas que venían eran:

- Uno para resolver con ecuación de primer grado.

- Uno para realizar un diagrama o figura.

- Uno con razones, proporciones y porcentajes.

- La interpretación de dos gráficas.

💬Desde mi opinión, los problemas de esta prueba sumativa, me resultaron más complejos que los vistos en la prueba anterior, ya que en esta última la mayoría de problemas debían ser resueltos con estrategias que involucraban un procedimiento matemático un tanto avanzado, y que por lo tanto, debíamos entender bien el problema para saber qué ecuación matemática plantear y cómo ir operándola hasta llegar al resultado, es decir, la incógnita que se nos pedía encontrar.

Por último, para la interpretación de gráficas, recomiendo observar detenidamente cada aspecto de la gráfica, pues nos podrían estar dando información esencial para lo que deseamos encontrar.

👤  Un ejemplo de algún problema en el examen es:

Un chef cobra Q1,500 por el servicio de catering básico; el 5.5% extra del precio anterior si el cliente desea loza incluida y el 8% extra si lo pide con servicio de bebidas frías.

a) ¿Cuánto dinero recibiría el chef si le piden un catering con loza incluida?

b) ¿Cuánto ganaría si le piden los dos servicios extra?

Paso 1: entender el problema.

Un chef cobra Q1,500 por catering más cierto porcentaje extra por servicio adicional. Nos pregunta cuánto dinero recibiría si se incluye ciertos servicios.

Paso 2: trazar una estrategia.

Razones, proporciones y porcentajes.

Paso 3: llevar a cabo la estrategia.

a) Con loza incluida (5.5% extra)

(Hacemos una regla de tres)

Q1,500     100%

     x          5.5%

R//: Q82.50 EXTRA  =>    Q1.500 + Q82.50 = Q1,582.50

b) Con loza (5.5%) y bebidas (8%) 

(Sumamos ambos porcentajes para luego operar con regla de 3)

5.5% + 8% = 13.5% 

(como es el 13.5% lo que se le va a adicionar al precio del catering, que equivale mi 100%, podríamos hacer la regla de 3 con el 113.5%, es decir, con el porcentaje ya añadido a mi precio total para no tener que sumarlo al finalizar la operación de regla de 3)

Q1,500    100%

     x       113.5%

R//: Q1,702.50 

Paso 4: revisar y comprobar.

Podemos sustituir los datos obtenidos por otros, para que al operarlos (al inverso) con cierta información obtenida, tengamos como respuesta alguno de los datos que se nos había dado originalmente.

👉A continuación se muestran unos vídeos para facilitar la comprensión del tema:

¿Qué son las proposiciones?

💢17 de junio, 2019

💭 El día de hoy vimos el concepto de una proposición, aprendimos a identificar cuando un enunciado es proposición o no, vimos los tipos de proposición y qué era la negación de éstas con su símbolo.

Esta clase se me facilitó, ya que para comprender mejor si un enunciado es proposición o no, solo debemos ver si podemos negarlo o verificarlo, si es así, sí es una proposición; de lo contrario, no lo es.

Y para identificar los tipos, solo debemos prestar mucha atención al momento de leer el enunciado, para entenderlo bien.

💬 Una proposición es el significado de un enunciado o idea, que se puede considerar solamente con un valor de verdad, ya sea: como un enunciado falso o como uno verdadero, pero jamás ambos.

Si no se puede calificar como verdadero o falso, no es proposición.

Tipos de proposición:

- Proposición abierta: donde el sujeto del enunciado no se especifica, por lo que, la información que nos presentan no es suficiente para saber su valor de verdad, pues no conocemos de quién o de qué se habla.

       Ejemplo: Él comió cinco tacos. (No sabemos de quién nos hablan).

- Proposiciones simples: se pueden representar por una sola variable, verdadera o falsa; pues solo es un resultado.

       Ejemplos:

p:  La semana tiene siete días. (Es verdadero).

q: 5 es un número par. (Es falso).

- Proposición compuesta: consta de dos o más enunciados simples (pueden ser con valores de verdad diferentes entre sí) y usan conectores entre ellos. Dependiendo qué conector sea se pueden clasificar y calificar así, como falsas o verdaderas.

       Ejemplo:

           p                             q        

Hoy es domingo y mañana será lunes.

Por último, las no proposiciones son aquellas oraciones interrogativas, exclamativas o imperativas.

Ejemplos: 

Arregla tu cuarto.

¡Qué felicidad!

¿Cuál es mejor?

Negación:  su símbolo es ( ~ ) y va antes de la proposición; volviendo su valor de verdad, lo contrario.

Ejemplo: no p 

~p

Si p fuera verdadero, ~p sería el negativo, es decir, sería falso; y viceversa.

Interpretación de información: lectura e interpretación de gráficas

💢 14 de junio 2019.

💭El día de hoy aprendimos a interpretar una gama de gráficas comprendida por: gráficas circulares, de barras, radiales, lineales y pictogramas. 
En lo personal, la gráfica que más se me dificultó interpretar fue la radial, por lo que recomiendo que la observen detalladamente.

👉Un aspecto sumamente importante a tomar en cuenta es que cada una de ellas mantiene diversas formas de expresar los datos y dependiendo de estos es que se escoge el tipo de gráfica que resulta más adecuado para la presentación de la información. 

💬En lo que respecta a la gráfica circular, su utilidad recae en la muestra de datos a partir de porcentajes, permitiendo la muestra de estos por medio de una distribución interna representando un hecho. 

Por otra parte, al referirse a la gráfica de barras, estas se emplean para ilustrar muestras agrupadas en intervalos. Su estética se encuentra conformada por rectángulos unidos a otros, en donde la superficie de cada barra es proporcional a la frecuencia de los valores que representa. Sus ejes representan un valor determinado y, por lo regular, el eje vertical expresa frecuencias y el eje horizontal el valor de las variables. Asimismo, la altura de cada rectángulo es proporcional a la frecuencia del intervalo respectivo. 

Ahora bien, al hablar de la gráfica de líneas, debe entenderse que estas muestran la relación entre dos variables cuantitativas. Además, se representan los valores en dos ejes cartesianos. Por su particularidad gráfica se recomienda su uso para la representación de series en el tiempo y es donde se muestran valores máximos y mínimos; asimismo, puede utilizarse para varias muestras en un diagrama. 

Por su lado, los pictogramas son diagramas que utilizan imágenes o símbolos para mostrar datos de una fácil de visualizar y comprender. Su estructura es semejante a la de una tabla en la que se denominan casillas que determinan datos específicos. 

Finalmente, las gráficas radiales son comparadores de los valores agregados de varias series de datos y estos muestran las permutaciones en los valores con relación a un punto central. Su estructura, por lo regular, es semejante a la de un rombo, circulo o pentágono que en su centro engloba los cuatro cuadrantes de un plano cartesiano. 

👤 A continuación, se mostrará un vídeo en donde se explica de mejor manera cómo interpretar y realizar ciertas gráficas: